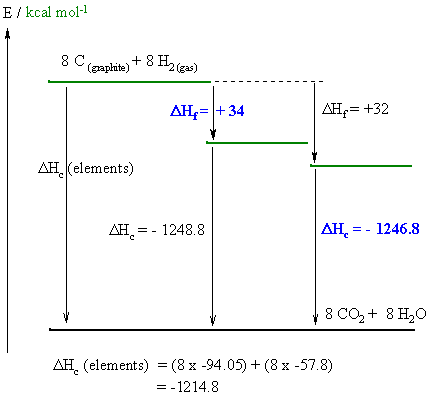
A reasonably straight forward calculation, but care needs to be taken to draw the diagram correctly and making sure you do the math correctly and pay close attention to the signs. One stumbling block for some students was that they didn't know what the different types of isomers meant and so didn't answer the questions asked !
First make sure to get the right molecular formula
: C8H16 and make sure to use balanced equations in the
Hess's law calculation.
Remember that the H16 comes from 8 H2 .
From the diagram :
(i) Hf I is given by : DHc
(elements) = DHc I + DHf
I therefore DHf I = -1214.8
--1248.8 = +34
(i) Hc II is given by : DHc
(elements) = DHc II + DHf
II therefore DHf II = -1214.8
- 32 = - 1246.8

How do we rationalise this ? The question asks for an analysis of the conformations. If we are talking about configurational isomers of 1,2-dimethylcyclohexane, we must be talking about the cis- and trans- systems. We are not talking about chair and boat isomers (these would be conformational isomers) or other substitution patterns including different branching patterns (these would be constitutional isomers). Note : E and Z terminology is only used for alkenes.
If we draw the cis-
and trans-
isomers out, then we should realise that the trans-
isomer can exist in two conformations, one where the methyl groups are
both axial and the other where they are both equatorial.
(Note a common error is the cis
and trans imply specfics
about axial and equatorial. They don'tbecause
it depends on the relative position of the groups, i.e. are
they 1,2- , 1,3- , 1,4- etc).
Axial substituents are destablised by a Van
der Waals interaction between the axial position and the other
axial
substituents on that face (in this case these are H atoms). Hence
substituents prefer to be equatorial. So the most stable system here
will
be the trans- isomer with
the two methyl groups equatorial. A careful analysis shows
that in both cases the angles between the methl groups is the same, 60
degrees.
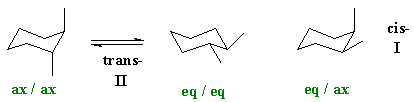
| cis- | trans- |